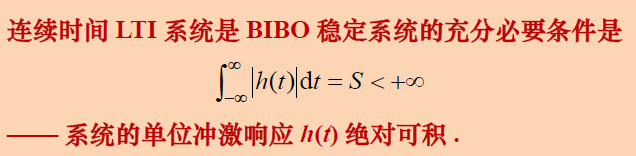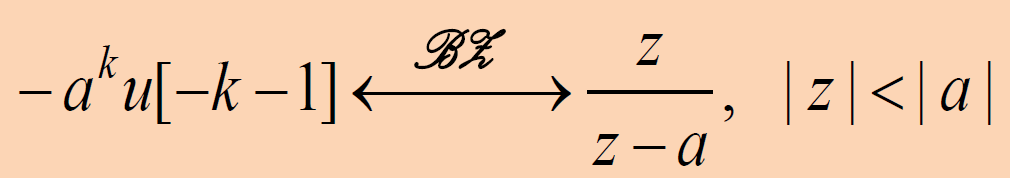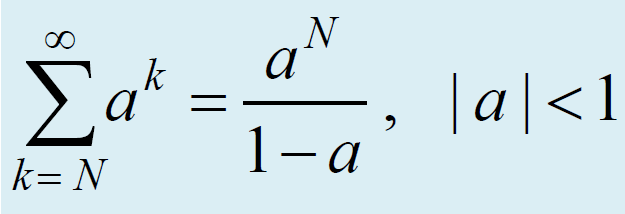信号与系统复习资料

信号与系统知识点和例题梳理

整理了一小部分知识点，和我自己学的不太扎实的题型。

信号的描述及分类

确定信号与随机信号

连续信号与离散信号

连续

1. 冲激信号$\delta(t)$
   信号大小一定要加括号
   筛选特性：$x(t)\delta(t-t_0)=x(t_0)\delta(t-t_0)$，若结果含有$x(t)\delta(t)$，必须化简一步。
   抽样特性：$\int_{\infty}^{\infty}x(t)\delta(t-t_0)=x(t_0)$
   展缩特性：$\delta(at)=\frac{1}{|a|}\delta(t)$
2. 阶跃信号$u(t)$
   不考虑$t=0$的值（该处的函数值没有定义）
3. 斜坡信号$r(t)$

离散

1. 冲激信号$\delta[k]$
   注意在$k=0$时函数值为1，而不是正无穷。标的时候不能加括号。
   $\delta[ak]=\delta[k]$，这点与连续的冲激函数不同。
2. 阶跃信号$u[k]$
   $k=0$时，函数值确定为1。
3. 斜坡信号$r[k]$

周期信号与非周期信号

连续

定义：$\forall x \in R$，存在正实数$T$，使得$x(t+nT)=x(t)$成立。则$T$是$x(t)$的周期。
最小正实数$T_0$称为基本周期
正弦信号$x(t)=A\sin(\omega_0 t+\theta)$的周期为：

$$T_0 = \frac{2\pi}{|\omega_0|}$$

离散

定义：$\forall k \in Z$，存在正整数$N$，使得$x[k+nN]=x[k]$成立。则$N$是$x[k]$的周期。
最小正实数$N_0$称为基本周期
离散正弦信号$x[k] = \sin(\Omega_0k)$不一定是周期信号！
若$\frac{|\Omega_0|}{2\pi}=\frac{m}{N}$为有理数（$m$和$N$都为不可约的正整数），则$N$为信号的周期。
虚指数序列$e^{j\Omega_0k}$的周期计算方法相同。

例：求下列离散序列的周期

(1)$x[k] = \sin(\frac{\pi}{5})$
解：

$$\frac{|\Omega_0|}{2\pi}=\frac{1}{10}$$

则周期为10

(2)$x[k] = \sin(\frac{4\pi}{11})$
解：

$$\frac{|\Omega_0|}{2\pi}=\frac{1}{10}$$

则周期为10

(3)以$T=0.4$抽样间隔对连续信号$sin(t)$抽样得到的离散信号
解：

$$sin(t)|_{t=kT}=sin(0.4k)$$

$$\frac{|\Omega_0|}{2\pi}=\frac{1}{5\pi}$$

为无理数，所以不是周期信号

能量信号和功率信号

归一化能量有限的称为能量信号
归一化功率有限的称为功率信号

例：判断下列信号是能量信号还是功率信号

（1）$x(t)=Ae^{-t}$
解：归一化能量

$$\int_{-\infty}^{+\infty}|Ae^{-t}|^2=-2A^2e^{-2t}|_{-\infty}^{+\infty}=\infty$$

归一化功率

$$\lim_{T\rightarrow\infty}(\frac{1}{2T}\int_{-T}^{T}|Ae^{-t}|^2)=\lim_{T\rightarrow\infty}(-2A^2e^{-2t}|_{-T}^{T})=\infty$$

既不是能量信号，也不是功率信号
（2）$x[k]=(\frac{4}{5})^k,k\ge 0$
解：归一化能量

$$\lim_{N\rightarrow\infty}\sum_{k=-N}^{N}|x[k]|^2=\lim_{N\rightarrow\infty}\sum_{k=0}^{N}(\frac{4}{5})^{2k}=\frac{1}{1-0.64}$$

归一化功率

$$\lim_{N\rightarrow\infty}\frac{1}{2N+1}\sum_{k=-N}^{N}|x[k]|^2=\lim_{N\rightarrow\infty}\frac{1}{2N+1}\sum_{k=0}^{N}(\frac{4}{5})^{2k}$$

$$=\lim_{N\rightarrow\infty}\frac{\frac{1}{1-0.64}}{2N+1}=0$$

是能量信号，也是功率信号（能量信号一定是功率信号）

系统的描述及分类

系统的描述

1. 输入输出描述
2. 状态变量描述

系统的分类和判断

离散、连续

显而易见

线性非线性

1. 均匀特性
   若$T{x(t)}=y(t)$，则$T(kx(t))=ky(t)$
   输入翻倍，输出也翻倍。
2. 叠加特性
   若$T\{x_1(t)\}=y_1(t)$，$T\{x_2(t)\}=y_2(t)$，则$T\{x_1(t)+x_2(t)\}=y_1(t)+y_2(y)$
   输入相加，输出也相加。
3. 综合表示
   若$T\{x_1(t)\}=y_1(t)$，$T\{x_2(t)\}=y_2(t)$，则$T\{\alpha x_1(t)+\beta x_2(t)\}=\alpha y_1(t)+\beta y_2(y)$
   输入线性组合，输出也线性组合。
4. 零输入和零状态线性
   含有初始状态的系统，若系统的响应可以分解为零输入和零状态，则需要分别求线性。只要两部分都线性，系统就线性。
   若系统的响应不可以被分解为零输入和零状态（例如：$y[k]=4y[0]·x[k]+3x[k]$），则一定不线性，因为初始状态不会受输入影响，输入线性组合不会改变初始状态，也就无法使得输出线性组合。

例：判断该系统是否为线性系统

（1）$y(t)=y(0)sin(2t)+\int_{0}^{t}x(\tau)d\tau$
解：

$$y_{zs}(t)=\int_{0}^{t}x(\tau)d\tau$$

$$y_{zi}(t)=y(0)sin(2t)$$

$$T_{zs}\{\alpha x_1(t)+\beta x_2(t)\}=\int_{0}^{t}\alpha x_1(\tau)+\beta x_2(\tau)d\tau$$

$$\alpha y_{zs1}(t)+\beta y_{zs2}(t)=\alpha\int_{0}^{t} x_1(\tau)+\beta\int_{0}^{t} x_2(\tau)d\tau$$

输入线性组合的响应与输出线性组合相等，具有零状态线性

$$T_{zi}\{\alpha y_1(0)+\beta y_2(0)\}=[\alpha y_1(0)+\beta y_2(0)]\sin(2t)$$

$$\alpha y_{zi1}(t)+\beta y_{zi2}(t)=\alpha y_1(0)\sin(2t)+\beta y_2(0)\sin(2t)$$

初始状态线性组合的响应与输出线性组合相等，具有零输入线性
综上，该系统具有线性
（2）$y[k]=2y[0]+6x^2[k]$
解：零输入响应$y_{zi}[k]=2y[0]$，显然线性

$$y_{zs}[k]=6x^2[k]$$

$$T_{zs}\{\alpha x_1[k]+\beta x_2[k]\}=6\alpha^2x_1^2[k]+12\alpha\beta x_1[k]x_2[k]+6\beta^2x_2^2[k]$$

$$\alpha y_{zi1}[k]+\beta y_{zi2}[k]=6\alpha^2x_1^2[k]+6\beta^2x_2^2[k]$$

二者并不相等，所以不具有零状态线性。
综上，该系统不具有线性

时变非时变

定义：非时变系统中，若$x(t)$产生的输出为$y(t)$，则输入$x(t-t_0)$产生的输出必为$y(t-t_0)$。离散同理。

LTI系统

具有线性和非时变性的系统成为线性非时变系统（Linear Time-Invariant System）。

1. 积分（求和）特性
   输入积分，输出也积分。
2. 微分（差分）特性
   输入微分，输出也微分。
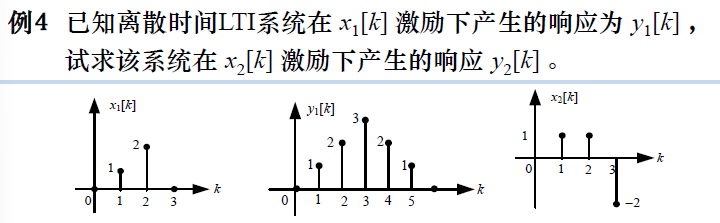
   这些特性可以用来根据已知的激励和响应，求线性组合、微分积分的激励产生的响应

因果非因果

任意时刻的输出，都不超前于系统的输入。
例如：$y[k]=2x[k+1]$，0时刻的输出由1时刻的输入决定，超前于输入，因此不是因果系统。

用单位冲激响应判断（只适用于LTI系统）

因果系统的 $H(s)$ ，则其收敛域为 $\text{Re}(s) > \sigma_0$（某个右半平面）。
因果离散系统，ROC 是以原点为中心某个圆周的外侧区域（即 $|z| > r_0$）

方法	连续系统	离散系统
冲激响应	$h(t)=0,\ t<0$	$h[k]=0,\ k<0$
复频域收敛域	$s$收敛域包括右半平面	$z$收敛域为某一圆外

稳定非稳定

任意有界的输入，其输出都是有界的。例如：$\int_{-\infty}^{t}x(\tau)d\tau$，输入为阶跃信号时，$t\rightarrow\infty$时，输出是无穷，不满足条件。不具有BIBO稳定性。

单位冲激响应判断（只适用于LTI系统）

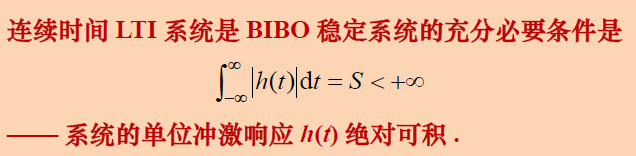
在复频域，连续时间LTI系统具有BIBO稳定性的充要条件是系统函数$H(s)$的收敛域包含$s$平面的虚轴，即收敛域$Re(s)>\sigma_0$且$\sigma_0<0$。
在复频域，离散时间LTI系统具有BIBO稳定性的充要条件是系统函数$H(z)$的收敛域包含$z$平面的单位圆，即$|z|<r_0$且$r_0>1$。

信号的基本运算

时域信号，所有的操作都是对自变量t或者x，而不是对括号内的整体。
先时移，再翻转/压缩/扩展

翻转

压缩/扩展

时移

例：

卷积

连续

$$x(t)*h(t)=\int_{-\infty}^{+\infty}x(\tau)h(t-\tau)d\tau$$

例：求$x(t)*h(t)$
(1)$x(t)=e^{-t}u(t),h(t)=e^{-2t}u(t-2)$

后面整理的比较仓促。

傅里叶变换性质

序号	性质名称	时域表达$x(t)$	频域表达$X(j\omega)$	说明
1	线性性	$ax_1(t)+bx_2(t)$	$aX_1(j\omega)+bX_2(j\omega)$	傅里叶变换是线性运算
2	时移性质	$x(t-t_0)$	$X(j\omega)e^{-j\omega t_0}$	时间延迟对应频域相位变化
3	频移性质	$x(t)e^{j\omega_0t}$	$X(j(\omega-\omega_0))$	调制使频谱移动
4	缩放性质	$x(at)$	$\frac{1}{a}X\left(j\frac{\omega}{a}\right)$	时间伸缩对应频率反向伸缩
5	微分性质	$\frac{d^nx(t)}{dt^n}$	$(j\omega)^nX(j\omega)$	导数变乘频率项
6	积分性质	$\int_{-\infty}^{t}x(\tau)\,d\tau$	$\frac{1}{j\omega}X(j\omega)+\pi X(0)\delta(\omega)$	时间积分对应频域除以$j\omega$
7	卷积性质	$x_1(t)*x_2(t)$	$X_1(j\omega)\cdot X_2(j\omega)$	时域卷积对应频域乘法
8	乘积性质	$x_1(t)\cdot x_2(t)$	$\frac{1}{2\pi}X_1(j\omega)*X_2(j\omega)$	时域乘法对应频域卷积

常见傅里叶变换对

原始信号 $x(t)$	傅里叶变换 $X(j\omega)$
$\cos(\omega_0 t)$	$\pi[\delta(\omega - \omega_0) + \delta(\omega + \omega_0)]$
$\sin(\omega_0 t)$	$j\pi[\delta(\omega + \omega_0) - \delta(\omega - \omega_0)]$
$\delta(t)$	$1$
$\delta(t - t_0)$	$e^{-j\omega t_0}$
$u(t)$	$\pi\delta(\omega) + \frac{1}{j\omega}$
$\cos(\omega_0 t)$	$\pi[\delta(\omega - \omega_0) + \delta(\omega + \omega_0)]$
$\sin(\omega_0 t)$	$j\pi[\delta(\omega + \omega_0) - \delta(\omega - \omega_0)]$
$e^{j\omega_0 t}$	$2\pi \delta(\omega - \omega_0)$
$e^{-a t} u(t),\ a > 0$	$\frac{1}{a + j\omega}$
$x(t) = u(t + T/2) - u(t - T/2)$	$T \cdot \text{Sa}\left( \frac{\omega T}{2} \right)$

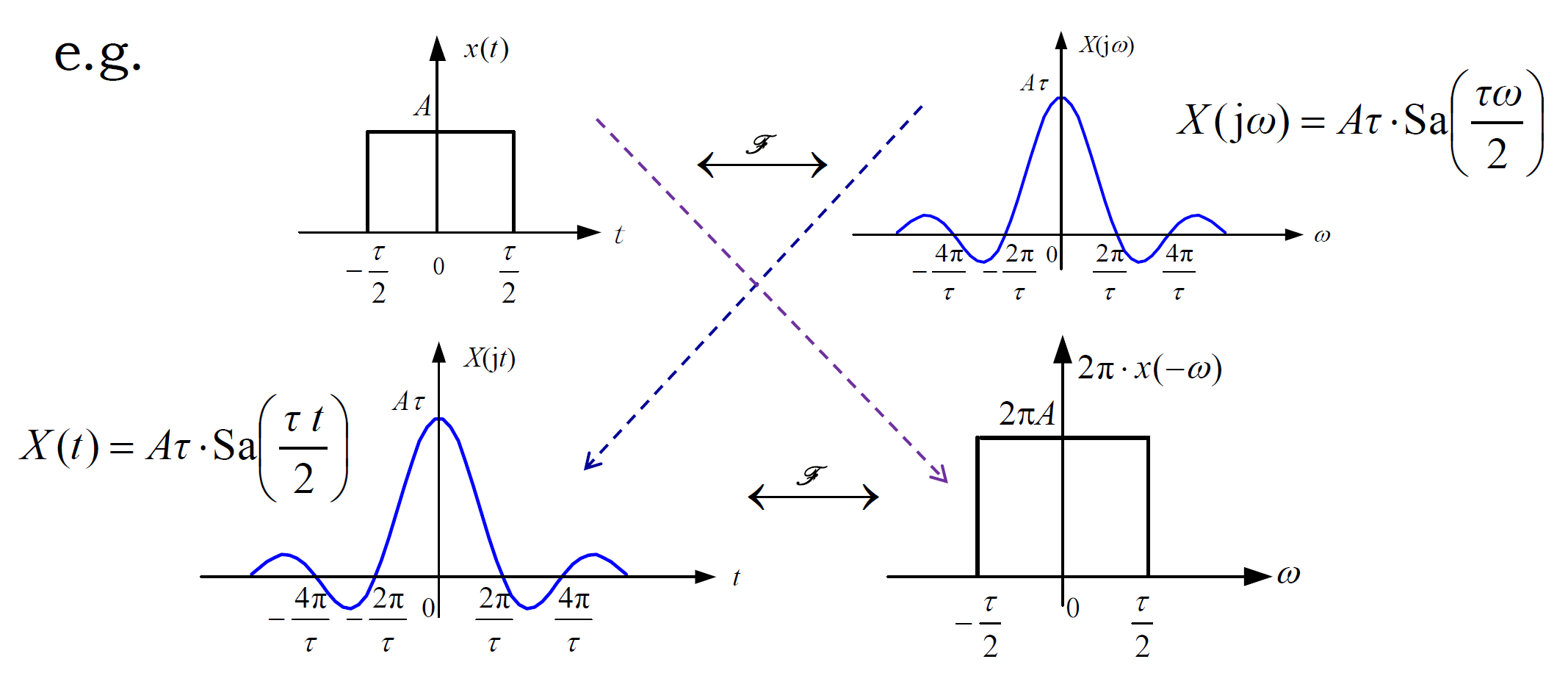
互易对称性

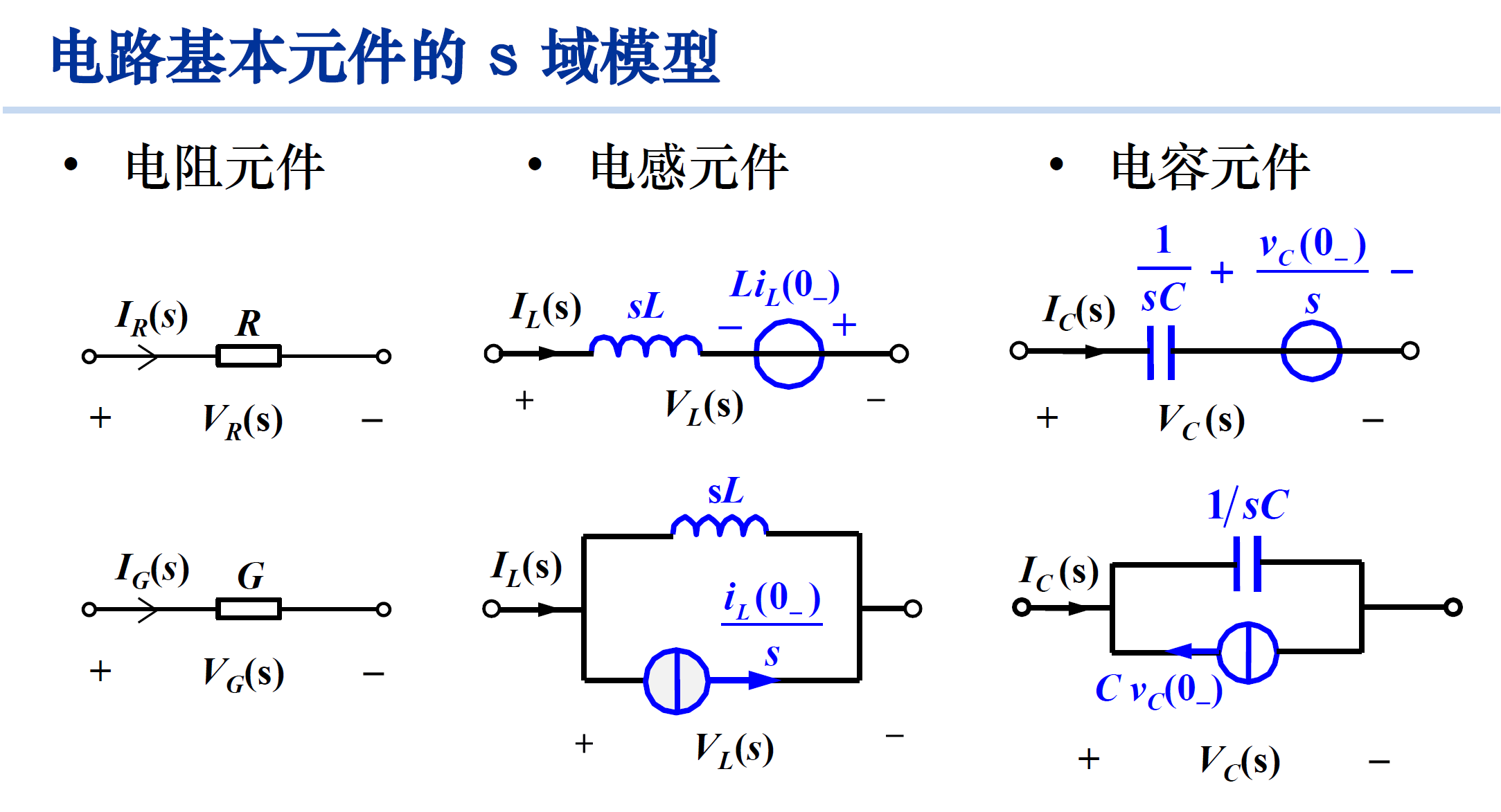
双边z变换

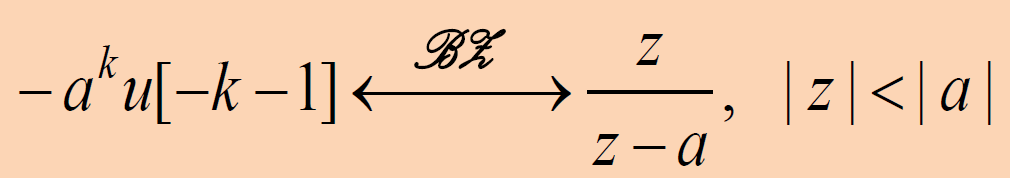
等比数列求和公式

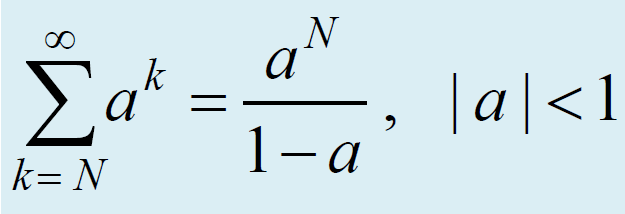
离散时间傅里叶变换

初值定理终值定理

连续（s域）

$$x(0^+)=\lim_{s\rightarrow+\infty}sX(s)$$

$$x(+\infty)=\lim_{s\rightarrow0}sX(s)$$

离散（z域）

$$x[0]=\lim_{z\rightarrow+\infty}X(z)$$

$$x[+\infty]=\lim_{z\rightarrow 1}(z-1)X(z)$$